What is a Graph?

From Wikipedia:

In mathematics, a graph is a representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges.

Simply put, a graph is just a bunch of points with links between them. A road map is a simple example: roads being edges, and intersections being vertices. In fact, Google maps uses graphs for just this purpose! Graphs are widely used in a wide variety of places. Facebook uses graphs to model your friend connections and likes. In fact, the entire internet is just a giant graph; websites act as vertices, with hyperlinks as edges. Graphs are highly useful structures, as they can be used to model many different types of situations, and as such, they will be the focus of this blog post. I am going to discuss one way to represent a graph in the Haskell programming language, and how to functionally solve a common problem using graphs. Graphs are often represented visually like this:

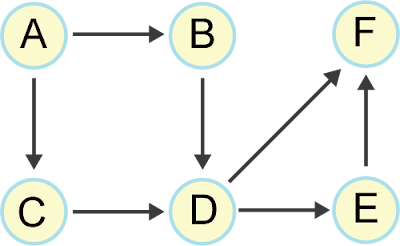
Graph representing abstract data

This graph links the first six letters of the alphabet in an arbitrary way. This data doesn’t really mean anything, but it will serve as a simple foray into the world of graphs, and provides an initial graph to work towards representing in Haskell. Let’s get right to it; here’s the data structure we’ll be using, along with some convenience methods:

module Graph(
  Graph(Graph),
  removeEdge,
  outbound,
  inbound
)where

data Graph a = Graph{ vertices :: [a], edges :: [(a, a)] } deriving Show

removeEdge :: (Eq a) => (a, a) -> Graph a -> Graph a
removeEdge x (Graph v e) = Graph v (filter (/=x) e)

connections :: (Eq a) => ((a, a) -> a) -> a -> Graph a -> [(a, a)]
connections f x (Graph _ e) = filter ((==x) . f) e

--outbound connections
outbound a = connections fst a

--inbound connections
inbound a = connections snd a

First we define the actual Graph a data type: It’s simply a set of vertices and edges in the form of 2-tuples (The tuple (a, b) connects vertex a to vertex b), which fits our definition. I’ve also defined the removeEdge method, which does just what you’d expect. The outbound and inbound functions find the outbound and inbound connections to any point in the graph, respectively. They make use of the polymorphic connections method in order to get this done in a small amount of code. Finally, the Graph module exports the relevant functions at the top of the file. Now that we’ve got our framework in order, we can go ahead and build the graph we mentioned above:

import Data.List --for later
import System.Environment --for later
import Graph

data Letter = A | B | C | D | E | F deriving (Show, Eq, Enum)

sample :: Graph Letter
sample = Graph [A,B,C,D,E,F] [(A, B), (A, C), (B, D), (C, D), (D, E), (D, F), (B, C), (F, E)]

We import the Graph module and define a simple Letter data type, then build our Graph from it. The set of vertices are the letters A, B, C, D, E, and F, and the edges are modeled as above. Now that we know how to build graphs, we can start modeling more important information with them.

Modeling Actual Scenarios using Graphs

Suppose some of the characters from NBC’s Parks and Recreationhave just finished competing in a dance competition, and we know the following about their rankings:

• Leslie beat April.
• April beat Ann.
• Ron beat April.
• Ron beat Ann.
• April beat Andy.
• Leslie beat Ron.
• Andy beat Jerry.
• Ron beat Andy.
• Ann beat Jerry.
• Leslie beat Andy.
• Ann beat Andy.

This is a little hard to mentally parse, so why don’t we model it as a graph to make it a little more readable? Each person can be represented as a vertex, with outgoing edges representing connections to the people they beat.

A graph of dance competition results

It would be nice to be able to be able to read scenarios like this from a text file containing the important data and parse it into a graph. Let’s go ahead and set up a function to do this for us, so we don’t have to hard-code each and every graph that we want to use: Here’s our data file, with a list of space-separated connections, one on each line:

Leslie Andy
April Andy
Ron Ann
Ron April
Ann Jerry
Ann Andy
Leslie April
Ron Andy
Leslie Ron
Andy Jerry
April Ann

And our parsing function:

graphFromFile :: String -> IO (Graph String)
graphFromFile f = do
  contents <- readFile f
  let info   = map words $ lines contents
      verts = nub . concat $ info
      conns  = map (\[a, b] -> (a, b)) info
      graph  = Graph verts conns
  return graph

The graphFromFile function takes a String and returns an IO (Graph String). The function reads a file, parses it into two important pieces: verts (the set of all unique strings in the file, or, our vertices) and conns (the set of connections between strings in the file). It then builds a Graph from this data, wraps it in the IO monad with return, and gives it back. Now you might have been wondering from the beginning of this section what the ranking from the dance competition was (maybe you even figured it out on your own!). How do we do this programmatically, using our graph?

Enter Topological Sort

Again, from Wikipedia:

In computer science, a topological sort of a directed graph is a linear ordering of itsvertices such that, for every edgeuv, u comes before v in the ordering.

In our case, this just means that each person must come before allof the people that he or she beat in the competition, in the ordering. The basic procedure for topological sort is as follows:

• L = {} –sorted list
• S = Set of vertices with no incoming connections
• while S is not empty:
  • for each vertex v in S with no incoming connections:
    • push v to L
    • for each edge e from v to u:
      • remove e from graph
      • if u has no more incoming connections, push u to S
• if edges still exist in the graph, error: there is at least one cycle in the graph
• Otherwise, return L

If you do not understand this, I urge you to work through topologically sorting a graph on paper first; it’s not too tough to understand once you’ve done it on paper, but can get a little confusing in psuedocode. The problem with this algorithm is that you see a ton of loops – control structures that we do not have in Haskell. Therefore, we must rely on recursion, folds, and maps to achieve what we want to do. Here’s how it looks:

tsort :: (Eq a) => Graph a -> [a]
tsort graph  = tsort' [] (noInbound graph) graph
  where noInbound (Graph v e) = filter (flip notElem $ map snd e) v
        tsort' l []    (Graph _ []) = reverse l
        tsort' l []    _            = error "There is at least one cycle in this graph."
        tsort' l (n:s) g            = tsort' (n:l) s' g'
          where outEdges = outbound n g
                outNodes = map snd outEdges
                g'       = foldr removeEdge g outEdges
                s'       = s ++ filter (null . flip inbound g') outNodes

Our tsort function first finds the elements in the graph with no incoming edges using the function noInbound. We pass this into a sub-routine tsort' that takes a sorted list l, a list of vertices with no incoming connections (n:s), and a graph g. We operate on the first element of the set of vertices with no incoming connections n, finding outEdges (the outgoing edges from n), and outNodes (the nodes that n points to). We build a new graph g' with the outEdges removed, and find the nodes in g' with no inbound connections, and add them to s. We then recursively call tsort' with these new parameters (and prepend our current n to the sorted list), until there are no more nodes to check. At this point, if the edge list in the graph is empty, all is well and we return the list of sorted elements. Otherwise, an error is thrown stating that there is at least one cycle in the graph. Now that we’ve got that, we’re ready to find out how everyone ranked in the dance competition!

> let danceOutcome = graphFromFile "people.txt" >>= \f -> return $ tsort f
> ["Leslie", "Ron", "April", "Ann", "Andy", "Jerry"]

(Of course Jerry lost!)

Conclusion

As you can see, Graphs are very useful data structures. They can be used to model a huge variety of things (see how many more you can come up with, they’re everywhere!). Topological sort in particular is a pretty remarkable algorithm, and can be applied in many different situations from the one above. For example, finding paths through college courses with prerequisites. It’s even used in UNIX systems to schedule processes according to their dependencies.

Hope you enjoyed the post!

Until next time,

Ben