Modeling and Simulating Markov Chain Evolution
In this post, I will describe and implement a small interface for modeling Markov chains and simulating their evolution in Haskell.
What is a Markov Chain?
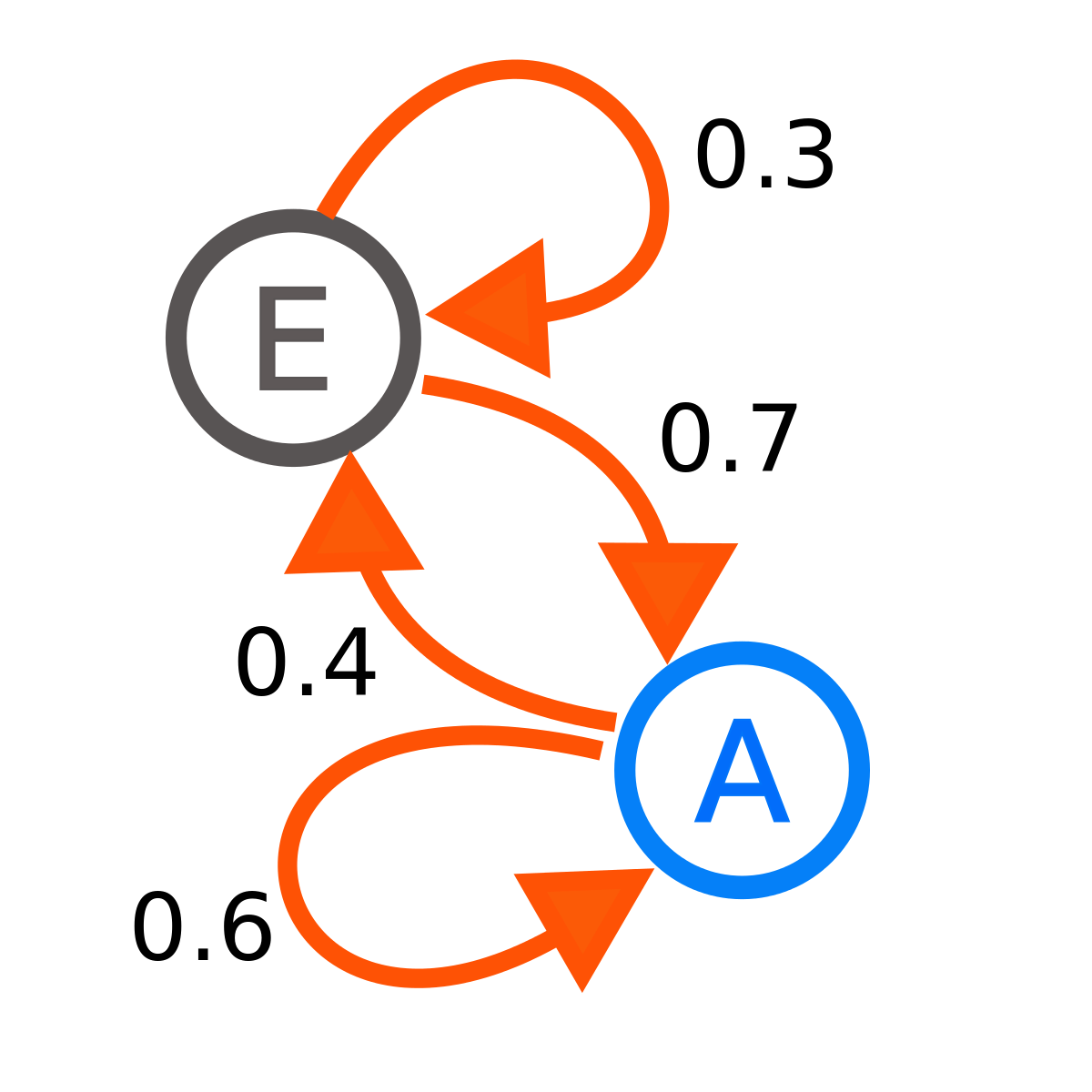
A simple two-state Markov chain.
image by Joxemai4.
A [discrete-time Markov chain (DTMC)](https://en.wikipedia.org/wiki/Markov_chain) is a mathematical system that probabalistically transitions between states using only its current state. A Markov chain can be thought of as a directed graph with probabilities for edges and states for vertices. The Markov chain on the right has two states, `E` and `A`. The diagram states that a Markov chain in state `E` will transition back to state `E` with probability `0.3`, and to state `A` with probability `0.7`, and similarly for `A`'s transitions. They can be used for a wide variety of applications in statistical modeling.
They can also be used to generate sentences similar to arbitrary blocks of text. We will explore this application towards the end of the post.
Aside: Weighted Random Generation
The first thing that comes to mind when I think of random generation is still the Prob data type described in LYAH. The MonadRandom library defines a data type Rand which works, in many ways, in the same way as the Prob data type does (with a bit of extension to produce a transormer, etc.). I won’t go into the full details of how this works, but the basic ideas is that, given a list of outcomes with weights, e.g.
[("Heads", 1), ("Tails", 1)]
we can – by wrapping it in Rand and giving it a random generator – produce a weighted random outcome, “Heads” or “Tails” with the desired weighting. For a concrete example, here’s a functional program written using the MonadRandom library.
import Control.Monad.Random
main :: IO ()
main = newStdGen >>= print . evalRand coinFlip
where coinFlip = uniform ["Heads", "Tails"]
uniform constructs a Rand from a list with a uniform distribution, i.e. with each member having the same weight. evalRand takes a Rand and a random generator (we’re using StdGen here with newStdGen) and spits out a weighted random object. Running this will print “Heads” about 50% of the time and “Tails” about 50% of the time.
Also of note is the fromList combinator, which takes a list of objects and their weights and constructs a Rand object. For example, replacing coinFlip with fromList [("Heads", 1), ("Tails", 1)] yields the same program as above.
Markov Chains: An Intermediate Representation
In order to model Markov chains, we essentially want to build a graph with weighted edges. We can model edge-weighted graphs using a HashMap from vertices to lists of edges, represented as (vertex, weight) pairs (the vertex the edge points to and its weight).
import qualified Data.HashMap.Lazy as M
import Data.Ratio
type MarkovI a = M.HashMap a (Maybe [(a, Rational)])
The MarkovI (I for “intermediate”) data type is a synonym for a lazy HashMap from a to a list of vertex-edge pairs. The only difference here is that we allow the list to be empty by using Maybe, which signifies an “end” state in the chain with no outgoing transitions. We could remove this wrapper and use an empty list to signify the same thing, but this representation works better with MonadRandom, since Rands can’t be empty, making the translation straightforward.
You might also be wondering why we need an intermediate representation for Markov chains in the first place. The reason for this is that we can’t arbitrarily insert extra objects/weights into Rands, and we’ll want to build up the mappings piecemeal. We need some intermediate structure to handle this functionality.
We can define functions to build up MarkovIs via insertion of objects:
insertMkvI :: (Hashable a, Eq a) => Rational -> a -> a -> MarkovI a -> MarkovI a
insertMkvI r k v mkv = M.insert k (Just $ case M.lookup k mkv of
Nothing -> [(v, r)]
Just xs -> case xs of
Nothing -> [(v, r)]
Just ys -> (v, r):ys) mkv
insertEnd :: (Hashable a, Eq a) => a -> MarkovI a -> MarkovI a
insertEnd k = M.insert k Nothing
insertMkvI inserts an edge into a MarkovI. Its first argument is the weight for the edge being inserted. Its next two arguments are the state objects to add a transition from/to, respectively, and the fourth is the MarkovI to insert into. insertEnd inserts a state with no outbound transitions into a Markov chain.
It is worth noting that the Rand object constructed from lists like this:
[(True, 1), (True, 1), (False, 1)]
do weight True twice as heavily as False. This will become important later, when talking about a sentence generator.
Markov Chains: Final Representation
The final representation of Markov chains simply turns those [(a, Rational)]s in MarkovI into true Rands.
import qualified Control.Monad.Random as R
newtype Markov g a = Markov{ getMarkov :: M.HashMap a (Maybe (R.Rand g a)) }
We can define a simple conversion function to construct Markovs from the intermediate representation by converting their distribution lists to Rands via fromList. This is straightforward because empty lists are represented as Nothing, so we don’t have to explicitly deal with that edge case when calling R.fromList, which would normally fail in such a case.
fromMarkovI :: RandomGen g => MarkovI a -> Markov g a
fromMarkovI = Markov . M.map (R.fromList <$>)
The first goal is to be able to – given a state and a random generator – transition to a new state probabalistically. The second goal is to be able to repeat this n times and track the states we pass through.
runMarkov1 accomplishes the first goal:
type Err = String
data Outcome g a =
Error Err
| Val a g
| End
deriving (Show, Eq)
runMarkov1 :: (R.RandomGen g, Hashable a, Eq a) => Markov g a -> g -> a -> Outcome g a
runMarkov1 mkv gen x = case M.lookup x (getMarkov mkv) of
Nothing -> Error "Internal error; cannot find value"
Just rs -> case flip R.runRand gen <$> rs of
Nothing -> End
Just (a, g) -> Val a g
First, if the state we’re looking for doesn’t exist, it is impossible to transition out of it, so the computation fails with an internal error. If not, we get a probablistic value out of the transition mappings from the state in question. If there aren’t any, we just End – we cannot transition, but don’t really want to throw an error. If there are values to choose from, we return one along with a new random generator, wrapped in Val.
Extending this to run n times isn’t too tough. It mostly consists of finagling data types into the representation we want.
runMarkov :: (R.RandomGen g, Hashable a, Eq a) => Integer -> Markov g a -> g -> a -> Either Err [a]
runMarkov n mkv gen x = go n
where
go m | m <= 0 = Right []
| otherwise = (x:) <$> case runMarkov1 mkv gen x of
Val a g -> runMarkov (n-1) mkv g a
End -> Right []
Error err -> Left err
If we hit an End, the simulation terminates because it can’t progress any further. If we get an error along the way, we wrap it in Left and return it. Otherwise, we run runMarkov1 repeatedly n times, starting from the previously computed state each time, and collecting the results into a list. If no errors occur, the result will be a list of states passed through while the simulation runs.
We can now define a fromList function, which builds up a Markov chain from mappings represented in list form.
fromList :: (Hashable a, Eq a, R.RandomGen g) => [(a, [(a, Rational)])] -> Markov g a
fromList = Markov . foldl' (flip $ uncurry ins) M.empty
where ins a b m = case b of
[] -> M.insert a Nothing m
_ -> M.insert a (Just $ R.fromList b) m
With this at our disposal, it’s easy to model and run the example Markov chain I mentioned earlier.
example :: Markov PureMT String
example = fromList [("E", [("E", 3), ("A", 7)]), ("A", [("E", 4), ("A", 6)])]
λ> :m + System.Random.Mersenne.Pure64
λ> gen <- newPureMT
λ> runMarkov 15 example gen "E"
Right ["E","A","A","A","E","E","A","A","A","A","A","A","E","E","A"]
The Markov chain passes through “A” a bit more often than “E”, which is to be expected from its definition.
Towards a Sentence Generator
The process of sentence generation using Markov chains is pretty simple: For each word in a “seed text,” find the probability of each other word proceeding it. Build a Markov chain out of these probabilities, using words as states, and run it a desired number of times. In order to do this, we’ll first need a utility function which takes pairs of elements (which will represent words along with the word following them in a “seed text”) and produces a Markov chain out of them.
insertMkvPairsInto :: (Hashable a, Eq a) => MarkovI a -> [(a, a)] -> MarkovI a
insertMkvPairsInto mkv [] = mkv
insertMkvPairsInto mkv ps = insertEnd lst $ foldl' (flip (uncurry (insertMkvI 1))) mkv ps
where lst = snd $ last ps
For each pair (x, y), we insert a transition x -> y with weight 1 into the Markov chain, and insert the final value in as an End. The reason this works is because of something I mentioned earlier: Rand handles distributions like [(True, 1), (True, 1), (False, 1)] properly. We build lists very similar to this one when processing a block of text for sentence generation, and when finally converting to Markov, all of that plumbing gets handled automatically. As a final note, we’ll use that End construct to mark the end of a sentence.
The next thing is actually building a MarkovI from a sentence – this can be done by zipping the list of its words with the tail of it and using the aforementioned function, like so:
import qualified Data.Text as T
wordPairs :: T.Text -> [(T.Text, T.Text)]
wordPairs = (zip <*> tail) . T.words
insertSentence :: MarkovI T.Text -> T.Text -> MarkovI T.Text
insertSentence mkv = insertMkvPairsInto mkv . wordPairs
Now, to build a Markov chain from a bunch of sentences (be it a paragraph, a book), we can just fold into an empty MarkovI and convert it from the intermediate representation:
fromSentences :: R.RandomGen g => [T.Text] -> Markov g T.Text
fromSentences = fromMarkovI . foldl' insertSentence M.empty
The rest is mostly plumbing:
{-# LANGUAGE OverloadedStrings #-}
import System.Random.Mersenne.Pure64
runFromSentences :: Int -> [T.Text] -> IO (Either Err T.Text)
runFromSentences n sentences = do
g <- newPureMT
let hds = map (head . T.words) sentences
seed <- R.uniform hds
return $ T.unwords <$> runMarkov n (fromSentences sentences) g seed
test :: [T.Text]
test = [
"I am a monster.",
"I am a rock star.",
"I want to go to Hawaii.",
"I want to eat a hamburger.",
"I have a really big headache.",
"Haskell is a fun language!",
"Go eat a big hamburger!",
"Markov chains are fun to use!"
]
We get a new PureMT to use for a generator, and grab a random word (from the beginning of a sentence) to use as the starting state. We then run a markov simulation, collecting the words we pass through, and finally call T.unwords on the result to build a sentence from the words in sequence. Running this yields some interesting statements (and a lot of nonsensical ones), for example:
λ> runFromSentences 10 test
Right "Haskell is a hamburger."
Right "Go eat a really big headache."
Right "I am a fun to go to go to eat"
Application: Rap Candy
As you might imagine, this type of thing gets more interesting when you’re working with a larger set of sentences. For me, I thought it would be fun(ny) to take lines from Eminem’s music as “sentences,” make tweet-sized snippets from them, and automate a twitter bot to post one every day. Most of the tweets are pretty nonsensical (and very vulgar), here’s one:
Now I'm on a magazine
Take a catastrophe for me
Cause of New sh*t, exclusive whoo kid
I'm the first king of danger, intertwine it
— rapcandy (@_rapcandy) August 1, 2014rapcandy is open source. Its Markov chain mechanism differs slightly from what was presented here, but the ideas are the same. It also includes a simple example of how to connect to Twitter using Haskell (which I’ll be covering separately in a short blog post soon), as well as web-scraper written in node that I used to download Eminem’s lyrics programmatically. Feel free to browse the code and follow @_rapcandy on Twitter.
I’ve also boxed up (most of) the code from this blog post into a small cabal package that you can use if you’d like to play around with your own Markov chain based applications. You can download markov-sim and browse its source here.