Graph Theory and The Handshake Problem
The Handshake Problem
The Handshake Problem is something of a classic in mathematics. I first heard about it in an algebra course I took in high school, and it’s stuck with me through the years. The question is this:
In a room containing \(n\) people, how many handshakes must take place for everyone to have shaken hands with everyone else?
The goal of this short blog post will be to present a solution to this problem using the concept of graphs.
The Complete Graph
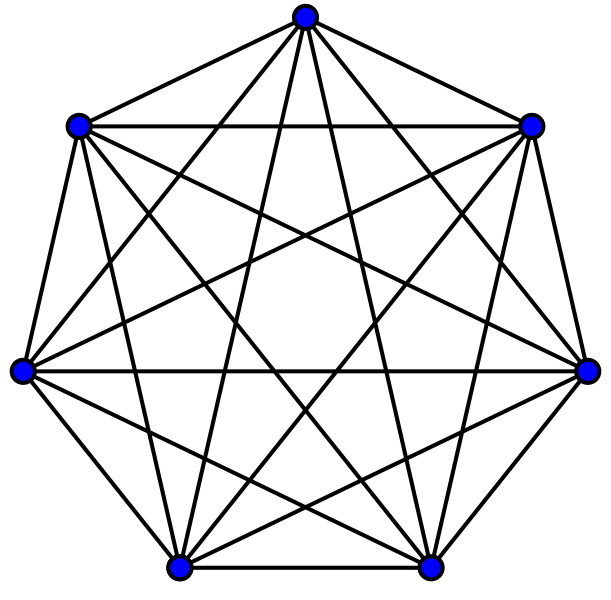
First, we must understand the idea of a complete graph. A complete graph is a graph such that each node is connected to every other node. A graphical example can be seen to the right. We can use the model of a complete graph to reason about the problem at hand. The nodes in the graph may represent the people in the room, while the connecting edges represent the handshakes that must take place. As such, the key to solving the Handshake Problem is to count the edges in a complete graph. But it would be silly to draw out a graph and count the edges one-by-one in order to solve this problem (and would take a very long time for large values of \(n\)), so we’ll use math!
The Solution
To find the solution, we have to make a few key observations. The easiest way to start out in this case is to map out the first few complete graphs and try to find a pattern: Let \(n\) = the number of nodes, \(e\) = the number of edges.
- \(n = 1 \Rightarrow e = 0\)
- \(n = 2 \Rightarrow e = 1\)
- \(n = 3 \Rightarrow e = 3\)
- \(n = 4 \Rightarrow e = 6\)
At this point, you may be noticing a pattern. As \(n\) increases, we’re adding \(n -1\) edges. This makes sense – each time a new node is introduced, it must connect to each node other than itself. In other words, \(n-1\) connections must be made. It follows that the number of the edges (\(e\)) in a complete graph with \(n\) vertices can be represented by the sum \((n-1) + (n-2) + \dots + 1 + 0\), or more compactly as: $$\sum_{i=1}^n i-1$$ You may already know from summation laws that this evaluates to \(\frac{n(n-1)}{2}\). Let’s prove it.
The Proof
Theorem: \(\forall n \in \mathbb{N} : \sum_{i=1}^{n} i-1 = \frac{n(n-1)}{2}\)
Proof:
Base case: Let \(n = 1\). Then, \(\frac{1(1-1)}{2} = \sum_{i=1}^1 i-1 = 0\).
Inductive step: Let \(n \in \mathbb{N}\). We need to prove that \(\frac{n(n-1)}{2} + n = \frac{n(n+1)}{2}\).
$$\begin{array} {lcl} \frac{n(n-1)}{2} + n & = & \frac{n(n-1)+2n}{2} \\ & = & \frac{n^2 - n + 2n}{2} \\ & = & \frac{n^2 + n}{2} \\ & = & \frac{n(n+1)}{2}■\end{array}$$
We can now use the theorem knowing it’s correct, and, in fact, provide a solution to the original problem. The answer to the Handshake Problem involving \(n\) people in a room is simply \(\frac{n(n-1)}{2}\). So, the next time someone asks you how many handshakes would have to take place in order for everyone in a room with 1029 people to shake each other’s hands, you can proudly answer “528906 handshakes!”
Until next time,
Ben